Java Double

Introduction

val a = 1f
val b = 0.9f
val r = a - b
println(r)  //  0.100000024

为什么会出现这个误差？接下来我们一步一步解答这个问题。

科学计数法

在数学中，采用科学计数法来近似表示一个极大或极小且位数较多的数。

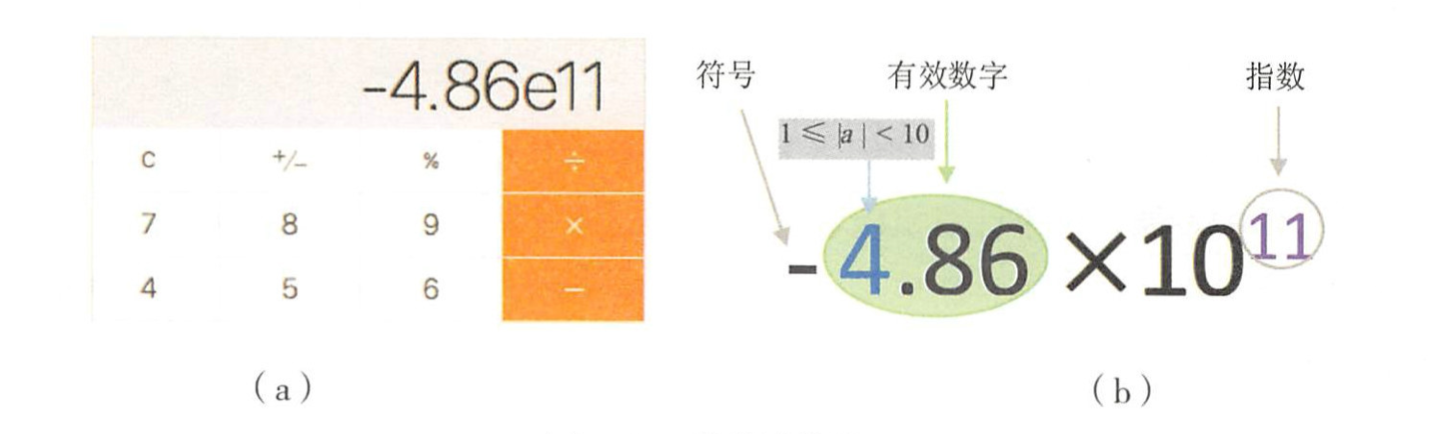
科学计数法组成部分：

有效数字：从第1个非零数字开始的全部数字；
指数：决定小数点的位置；
符号：表示正负数。

科学计数法可以唯一的表示任何一个数字，且所占用的存储空间会更少。浮点数表示方式：

存储时的组成部分：

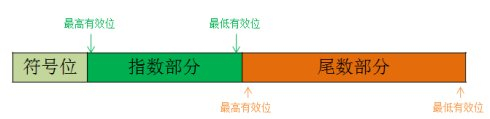
Float类型的内存分布：

Double类型的内存分布：

目前业界流行的浮点数标准是 IEEE754，规定了4种浮点数类型：

单精度
双精度
延伸单精度
延伸双精度

其中前两种类型是最常用的。

单精度

数制从十进制到二进制，还要考虑内存硬件设备的实现方式。指数称为”阶码”，有效数字称为”尾数”。所以用于存储符号、阶码、尾数的二进制位分别称为符号位、阶码位、尾数位。

符号位

在最高二进制位上分配1位表示浮点数的符号，0表示正数，1表示负数。

阶码位

在符号位右侧分配8位用来存储指数，IEEE754 标准规定阶码位存储的是指数对应的移码，而不是指数的原码或补码。

尾数位

最右侧分配连续的23位用来存储有效数字，IEEE754 标准规定尾数以原码表示。

正指数和有效数字的最大值决定了32位存储空间能够表示浮点数的十进制最大值。

指数最大值为2^127 约等于 1.7 x 10^38。

有效数字部分最大值是二进制的 1.11···1(小数点后23个1)，是个无限接近于2的数字，所以得到最大的十进制数为2 × 1.7 × 10^38，再加上最左1位的符号，最终得到32位浮点数最大值为 3.4e+38。

为什么8位阶码的偏置为127？

8位移码的取值范围为0~255（00000000~11111111），但在浮点数的阶码中，00000000与11111111被保留用作特殊情况，所以阶码可用范围只有1~254，总共有254个值。

8位有符号数取值范围为-128~+127（10000000~01111111），这里的二进制用补码表示，其中特别规定补码10000000没有原码，为-128的补码，总共有256个值。

如果采用偏置128，在表达+127(2的7次方=127)时会产生上溢（移码11111111被保留），所以在阶码中偏置为（128-1），与此同时，在表达-127时会产生下溢（移码00000000被保留），所以阶码中去掉-127与-128，取值范围为-126~127，总共254个值。

原码、补码、反码

计算机保存最原始的数字，不区分正负数，即无符号数字。如果我们在内存分配4位(bit)去存放无符号数字，是下面这样子的：

十进制	二进制
0	0000
1	0001
2	0010
3	0011
4	0100
5	0101

后来在生活中为了表示“欠别人钱”这个概念，就从无符号数中，划分出了“正数”和“负数”。为了表示正与负，人们发明了”原码”，把生活应该有的正负概念，原原本本的表示出来。

正数	二进制	负数	二进制
0	0000	-0	1000
1	0001	-1	1001
2	0010	-2	1010

但使用“原码”储存的方式，方便了看的人类，却苦了计算机。们希望(+1)和(-1)相加是0，但计算机只能算出0001+1001=1010(-2)，这个结果并不是我们想要的。此外，0的表示有两种方式：+0 和 -0。

为了解决”正负相加等于0”的问题，在”原码”的基础上，人们发明了”反码”。“反码”表示方式是用来处理负数的，符号位置不变，其余位置相反：

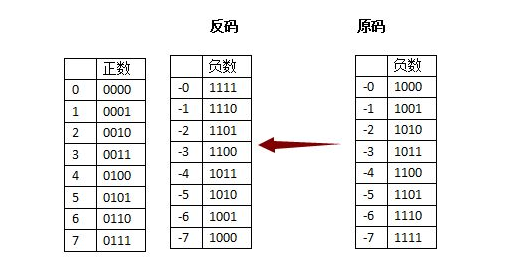
当“原码”变成“反码”时，完美的解决了“正负相加等于0”的问题。+1 和 -1 相加，变成了0001 + 1101 = 1111，刚好反码表示方式中，1111象征-0。

人们总是进益求精，历史遗留下来的问题—— 有两个零存在：+0 和 -0，我们希望只有一个0，所以发明了”补码”，同样是针对”负数”做处理的。

“补码”的意思是，从原来”反码”的基础上，补充一个新的代码：+1。

ß

有得必有失，在补一位1的时候，要丢掉最高位。

我们要处理”反码”中的”-0”，当1111再补上一个1之后，变成了10000，丢掉最高位就是0000，刚好和左边正数的0相同。

这样就解决了+0和-0同时存在的问题，另外”正负数相加等于0”的问题，同样得到满足：

例如，3 和 -3 相加，0011 + 1101 = 10000，丢掉最高位，就是0000(0)。

同样有失必有得，我们失去了-0，收获了-8。

#### Range

基本类型：int 二进制位数：32
包装类：java.lang.Integer
最小值：Integer.MIN_VALUE= -2147483648 （-2的31次方）
最大值：Integer.MAX_VALUE= 2147483647 （2的31次方-1）

基本类型：short 二进制位数：16
包装类：java.lang.Short
最小值：Short.MIN_VALUE=-32768 （-2的15此方）
最大值：Short.MAX_VALUE=32767 （2的15次方-1）

基本类型：long 二进制位数：64
包装类：java.lang.Long
最小值：Long.MIN_VALUE=-9223372036854775808 （-2的63次方）
最大值：Long.MAX_VALUE=9223372036854775807 （2的63次方-1）

基本类型：float 二进制位数：32
包装类：java.lang.Float
最小值：Float.MIN_VALUE=1.4E-45 （2的-149次方）
最大值：Float.MAX_VALUE=3.4028235E38 （2的128次方-1）

基本类型：double 二进制位数：64
包装类：java.lang.Double
最小值：Double.MIN_VALUE=4.9E-324 （2的-1074次方）
最大值：Double.MAX_VALUE=1.7976931348623157E308 （2的1024次方-1）

**
### Memory Usage

- Double: 8 Byte，range(1.4E-45 ~ 3.4028235E38)
- Float: 4 Byte，range(4.9E-324 ~ 1.7976931348623157E308)

**
### Comparison

#### Check whether value is zero

1
2
3

public boolean isZero(double value, double threshold){
    return value >= -threshold && value <= threshold;
}

Case - Simple comparison

First look at the simple comparison to understand what exactly is wrong with comparing double with == operator. In given program, I am creating same floating point number (i.e. 1.1) using two methods:

Add .1, 11 times.
Multiply .1 to 11.

In theory, both operations should produce the number 1.1. And when we compare the results of both methods, it should match.

//  Method 1
var f1 = .0
for (i in 1..11) {
    f1 += .1
}
//  It's acutally 1.1
//  f1 is computed to 1.0999999999999999. Its exactly the problem which rounding off causes internally. 
//  That’s why, floating point comparison with '==' operator is not recommended.

//  Method 2
val f2 = .1 * 11

println("f1 $f1, f2 $f2")
println("f1 == f2 -> ${f1 == f2}")

Output：

1 2	f1 1.0999999999999999, f2 1.1 f1 == f2 -> false

Use BigDecimal

//Method 1
var f1 = BigDecimal("0.0")
val pointOne = BigDecimal("0.1")
for (i in 1..11) {
    f1 = f1.add(pointOne)
}

//Method 2
var f2 = BigDecimal("0.1")
val eleven = BigDecimal("11")
f2 = f2.multiply(eleven)

println("f1 $f1, f2 $f2")
println("f1.compareTo(f2) -> ${f1.compareTo(f2) == 0}")

Output：

1 2	f1 1.1, f2 1.1 f1.compareTo(f2) -> true

Case - Threshold based comparison <— Recommended

Using programming, we cannot change the way these floating point numbers are stored or computed. So we have to adapt a solution where we agree that a determine the differences in both values which we can tolerate and still consider the numbers equal. This agreed upon difference in values is called the threshold or epsilon.

So now to use ‘threshold based floating point comparison‘, we can use the Math.abs() method to compute a difference between the two numbers and compare the difference to a threshold value.

val threshold = 0.0001
//Method 1
var f1 = .0
for (i in 1..11) {
    f1 += .1
}

//Method 2
val f2 = .1 * 11

println("f1 $f1, f2 $f2")
println("f1 == f2 -> ${Math.abs(f1 - f2) < threshold}")

Output：

1 2	f1 1.0999999999999999, f2 1.1 f1 == f2 -> true

Case - Compare with BigDecimal <— Recommended

In BigDecimal class, you can specify the rounding mode and exact precision which you want to use. Using the exact precision limit, rounding errors are mostly solved.

Best part is that BigDecimal numbers are immutable i.e. if you create a BigDecimal BD with value “1.23”, that object will remain “1.23” and can never be changed. This class provide many methods which can be used to do numerical operations on it’s value.

You can use it’s compareTo() method to compare to BigDecimal numbers. It ignore the scale while comparing.

Special Note：Never use the equals() method to compare BigDecimal instances. That is because this equals function will compare the scale. If the scale is different, equals() will return false, even if they are the same number mathematically.

val a = BigDecimal("2.00")
val b = BigDecimal("2.0")

println("a == b --> ${a == b}")
println("a.compareTo(b) --> ${a.compareTo(b) == 0}")

Output：

1 2	a == b --> false a.compareTo(b) --> true

NaN and INFINITY

Once a NaN always a NaN
Double.MAX_VALUE overflow into POSITIVE_INFINITY, The same goes for Double.MIN_VALUE except that it will overflow to Double.NEGATIVE_INFINITY.

NaN(Not a Number，非数)是计算机科学中数值数据类型的一类值，表示未定义或不可表示的值。常在浮点数运算中使用。

返回NaN的运算：

至少有一个參数是NaN的运算；
不定式：
- 除法运算：0/0、∞/∞、∞/(−∞)、(−∞)/∞、(−∞)/(−∞)
- 乘法运算：0×∞、0×−∞
- 加法运算：∞ + (−∞)、(−∞) + ∞
- 减法运算：∞ - ∞、(−∞) - (−∞)
- 指數運算：0^0、∞^0、1^∞、∞^(−∞)
产生复数结果的实数运算：对负数进行开偶次方的运算；对负数（包含−∞）进行对数运算；对正弦或餘弦到达域以外的数进行反正弦或反餘弦运算；

NaN

val result = Math.sqrt(-1.0)
println("Math.sqrt(-1.0) -> $result")
println("Double.NaN == result -> ${result.isNaN()}")
println("Double.NEGATIVE_INFINITY == result -> ${Double.NEGATIVE_INFINITY == result}")
println("Double.POSITIVE_INFINITY == result -> ${Double.POSITIVE_INFINITY == result}")

Output：

Math.sqrt(-1.0) -> NaN
Double.NaN == result -> true
Double.NEGATIVE_INFINITY == result -> false
Double.POSITIVE_INFINITY == result -> false

NEGATIVE_INFINITY

val result = -Double.MAX_VALUE * Double.MAX_VALUE
println("Double.MAX_VALUE * Double.MAX_VALUE -> $result")
println("Double.NaN == result -> ${result.isNaN()}")
println("Double.NEGATIVE_INFINITY == result -> ${Double.NEGATIVE_INFINITY == result}")
println("Double.POSITIVE_INFINITY == result -> ${Double.POSITIVE_INFINITY == result}")

Output：

-Double.MAX_VALUE * Double.MAX_VALUE -> -Infinity
Double.NaN == result -> false
Double.NEGATIVE_INFINITY == result -> true
Double.POSITIVE_INFINITY == result -> false

POSITIVE_INFINITY

val result = 5.0 / 0
println("5.0 / 0 -> $result")
println("isNaN -> ${result.isNaN()}")
println("Double.NEGATIVE_INFINITY == result -> ${Double.NEGATIVE_INFINITY == result}")
println("Double.POSITIVE_INFINITY == result -> ${Double.POSITIVE_INFINITY == result}")

Output：

5.0 / 0 -> Infinity
isNaN -> false
Double.NEGATIVE_INFINITY == result -> false
Double.POSITIVE_INFINITY == result -> true

Python Java Android Django Web -> sulang357159@gmail.com

Java Double

Introduction

科学计数法

单精度

为什么8位阶码的偏置为127？

原码、补码、反码

Case - Simple comparison

Case - Threshold based comparison <— Recommended

Case - Compare with BigDecimal <— Recommended

NaN and INFINITY

NaN

NEGATIVE_INFINITY

POSITIVE_INFINITY

Reference