Tree Feature
- 一个节点,即只有根节点,也可以是一棵树
- 其中任何一个节点与下面所有节点构成的树称为子树
- 根节点没有父节点,而子叶节点没有子节点
- 除根节点外,任何节点有且仅有一个父节点
- 任何节点可以有0~n个子节点
- 高度与深度的区别:叶子节点定义高度为1
- 高度:从节点到其子叶节点经过的最长路径
- 深度:从根节点往下到叶节点最长路径(根节点为1)
- 相同深度的节点,高度不一定相同
Binary Search Tree(二叉查找树)
遍历方式
- 前序遍历
- 中序遍历
- 后序遍历
AVL(平衡二叉树)
一种平衡二叉查找树,增加和删除节点后通过树形旋转重新达到平衡。
一颗完美平衡的树查找树中,所有空节点到根节点的距离应该是相同的。
特性:
- 树的左右高度差不能超过1
- 任何往下递归的左子树与右子树,必须符合第一条性质
- 没有任何节点的空树或只有根节点的树也是平衡二叉树
在每一次插入数值之后,树的平衡性都可能被破坏,这时可以通过一个简单的操作来矫正平衡–旋转。
旋转的目的就是减少高度,通过降低整棵树的高度来平衡。哪边的树高,就把那边的树向上旋转。
旋转操作
- 所谓的左旋和右旋都是以子树为原点的:如b是a的子树,那么旋转就围绕b来进行。
- 如果b是a的左子树,那么就围绕b将a向右旋转,看着就像是a直接掉下来了,掉成了b的右子树。
- 如果b是a的右子树,那么就围绕b将a向左旋转,看着就像是a直接掉下来了,掉成了b的左子树。
旋转类型
- LL:在a的左子树根节点的左子树上插入节点而破坏平衡,旋转方式-右旋转
- RR:在a的右子树根节点的右子树上插入节点而破坏平衡,旋转方式-左旋转
- LR:在a的左子树根节点的右子树上插入节点而破坏平衡,旋转方式-先左后右
- RL:在a的右子树根节点的左子树上插入节点而破坏平衡,旋转方式-先右后左
LL
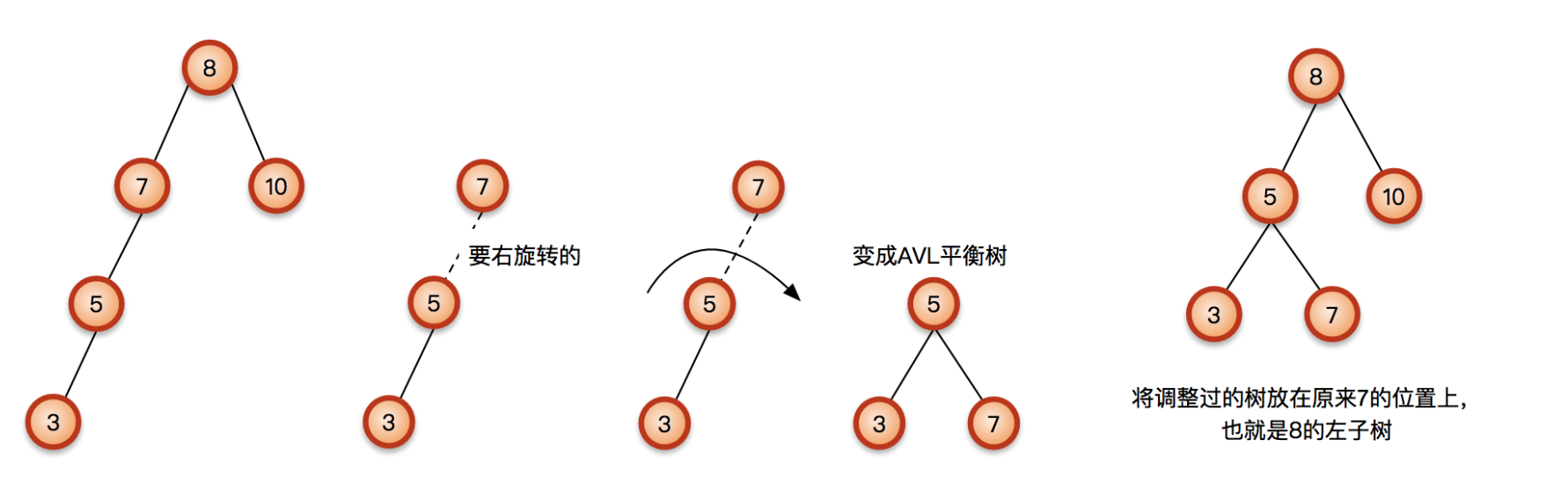
此时,节点7的左子树高度为2,右子树为0,则两边的差值超过1。
围绕节点5进行右旋转,因为节点5没有右子节点,此时可以直接把节点7设置为节点5的右子节点。需要注意的是,当调节完当前节点的平衡后,需要向上检查是否有节点出现不平衡的现象。
如果节点5已经存在右子树(节点7是节点5的父节点,肯定比节点5大,即也比节点5的右子节点大),此时节点7如何处理?请看下图
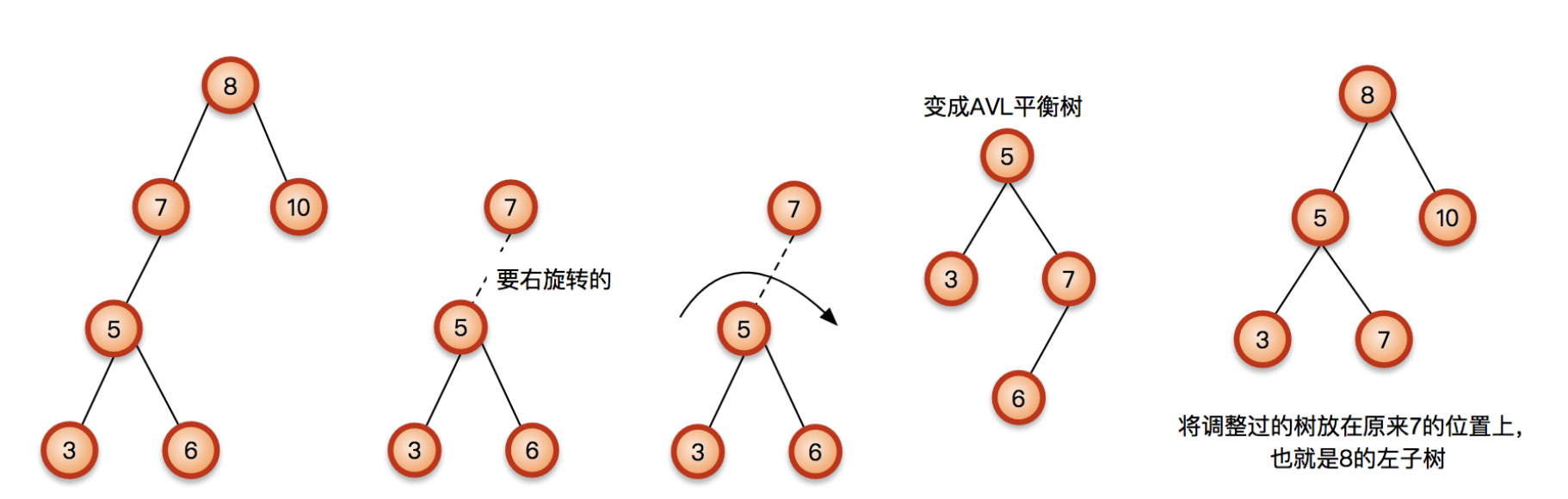
仍然针对节点5进行右旋,节点7仍然为节点5的右子树,节点6成为节点7的左子树,此时节点5已经平衡。但是当我们再看节点8的时候,节点8却失衡了。
RR
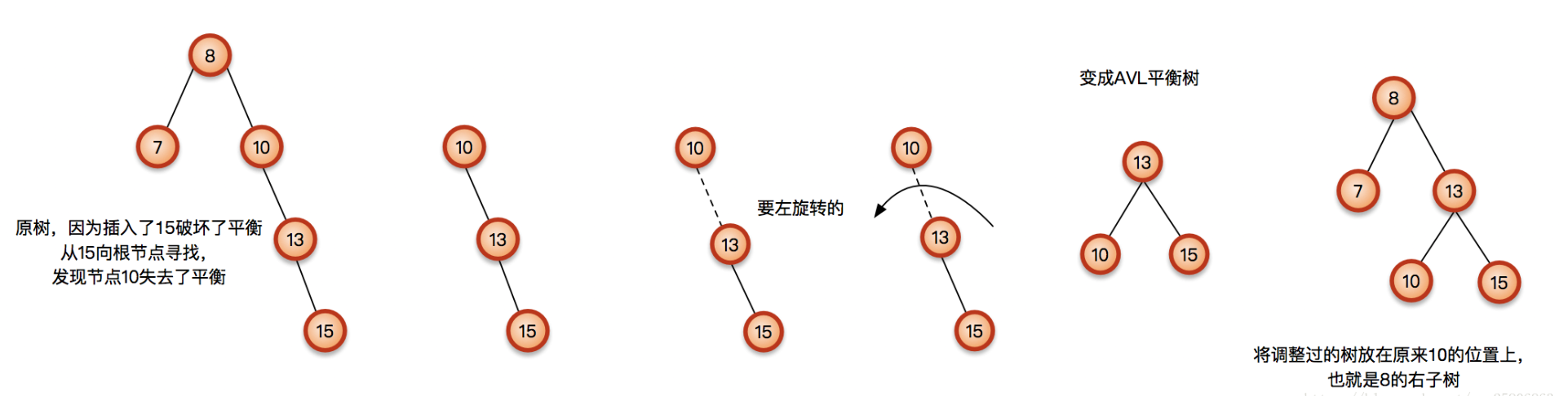
如果节点13已经有左子树,怎么办?
LR
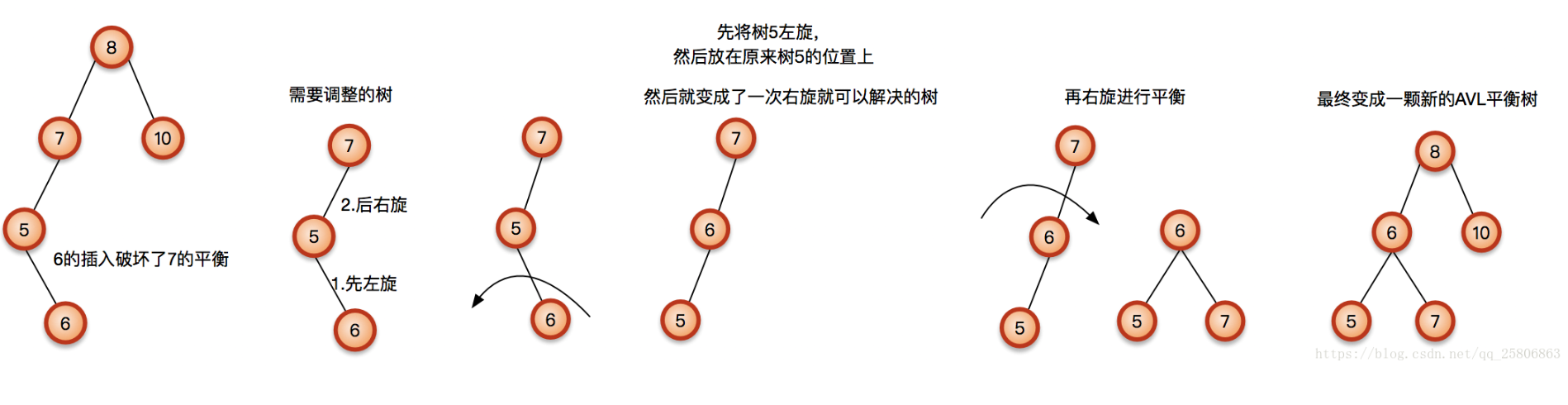
如果节点5已经有左子树,怎么办?
红黑树
应用场景对比
红黑树与AVL树
- 频繁的插入和删除,红黑树更加适合
- 低频修改和大量查询,AVL树更加适合